Eisen's Blog
Python Data Science, NumPy 2
2017 March-31
这篇文章延续Python Data Science, NumPy 1,介绍广播、高级索引以及数组排序。
广播
广播是在长度不同的数组上执行 ufunc(例如,加法,减法,乘法等)的一组规则。
对于大小相同的 NumPy 数组是逐个元素执行计算的:
a = np.array([0, 1, 2])
b = np.array([5, 5, 5])
a + b
# array([5, 6, 7])广播允许对不同大小的数组执行这些操作 - 例如,我们可以将一个标量(想象它是一个 0 维数组)和一个数组相加:
a + 5
# array([5, 6, 7])我们可以认为是这个操作首先把 5 转换为了数组 [5, 5, 5] 然后进行运算。NumPy 广播在实际运算中并没有这么做,但是我们可以借用这个思路来理解广播。
当然,对于更高维的数组也是可以的:
M = np.ones((3, 3))
M + a
# array([[ 1., 2., 3.],
# [ 1., 2., 3.],
# [ 1., 2., 3.]])一维数组 a 在第二维被拉伸(或者说是在第二维被广播)以便匹配 M 的维度。
还有更复杂的情况:即两个数组各自广播后计算:
a = np.arange(3)
b = np.arange(3)[:, np.newaxis]
a + b
# array([[0, 1, 2],
# [1, 2, 3],
# [2, 3, 4]])事实上,NumPy 是严格按照一些规则进行广播运算的:
- 规则1:如果连个数组的维度不同,那么维度较少的数组在自己当前维度的前面填充长度为 1 的维度。
- 规则2:如果两个数组任意一个维度的长度不符,那么在这个维度上长度为 1 的那个数组在该维度上进行拉伸,即填充同样的数据以适应另一个数组。
- 规则3:如果任意维度上长度不等,但两个数组在该维度的长度都不是 1,则报错
下面用几个例子进行说明。
示例 1
M = np.ones((2, 3))
a = np.arange(3)
M + a其中
- M.shape = (2, 3)
- a.shape = (3)
按照规则 1 a 的维度少,在其前面补充维度:
- a.shape -> (1, 3)
按照规则 2 第一维两者不同,所以对 a 进行拉伸:
- a.shape -> (2, 3)
然后再进行相加。
示例 2
a = np.arange(3).reshape((3, 1))
b = np.arange(3)- a.shape = (3, 1)
- b.shape = (3)
按照规则 1 b 扩充维度
- b.shape = (1, 3)
按照规则 2 长度为 1 的维度扩充:
- a.shape = (3, 3)
- b.shape = (3, 3)
a + b
# array([[0, 1, 2],
# [1, 2, 3],
# [2, 3, 4]])示例 3
M = np.ones((3, 2))
a = np.arange(3)- M.shape = (3, 2)
- a.shape = (3)
按照规则 1 扩充 a 的维度
- a.shape = (1, 3)
按照规则 2 a 被拉伸
- M.shape = (3, 2)
- a.shape = (3, 3)
然而此时两者的第二维没有一个为 1 但又不相当,按照规则 3 报错。
比较、掩码、布尔运算
上一部分介绍了 NumPy 有很多向量化快速运算的 universal functions,但是只介绍了算术运算的那些 ufuncs 实际上还有很多布尔运算的 ufuncs。
x = np.array([1, 2, 3, 4, 5])
x < 3
# array([ True, True, False, False, False], dtype=bool)
x == 3
# array([False, False, True, False, False], dtype=bool)可以看到这些运算的结果是一个布尔类型的长度相同的数组。布尔数组可以用于很多便捷的运算。
x = np.array([[5, 0, 3, 3], [7, 9, 3, 5], [2, 4, 7, 6]])
np.count_nonzero(x < 6)
# 8
np.sum(x < 6)
# 8其中 np.count_nonzero 可以用来计算 True 元素的个数,当然还可以用 np.sum 达到同样的目的,因为 False 会被认为是 0 而 True 会被转换为 1。
还有一些其他类似的操作:
np.any(x > 8)
# True
np.all(x < 10)
# True当然,这些运算都可以添加 axis 参数按照不同的轴进行运算。
np.all(x < 8, axis=1)
# array([ True, False, True], dtype=bool)注意 Python 有内置的 sum() any() 和 all() 函数,它们和 NumPy 中的运算略有区别,尤其是在用于多维数组的情况。一定要确保自己用的是 np.sum() np.any() 以及 np.all()。
处理基本的 > < != == >= <= 之外,还可以用 &(与) |(或) ^(异或) ~(否) 进行复合布尔运算。比如
np.sum((inches > 0.5) & (inches < 1))就是 inches > 0.5 与 inches < 1 的 与 操作。注意考虑到运算符的优先级,这里的两个括号是必须的。
在前面的部分我们看到可以直接对布尔数组进行聚合。一个更强大的方式是使用布尔数组作为掩码来获取数据本身的特定子集。回到之前的 x 数组,假设我们想要一个数组中所有小于 5 的数据,我们可以这么做:
x[x < 5]结果返回一个一维数组,其元素为满足条件式的所有数据;换言之获取的是所谓索引为 True 的元素。这些运算可以让我们轻易的获取想要的结果。
Fancy Indexing
Fancing indexing 的概念非常简单:用索引数组访问多个数组元素。举一个例子:
import numpy as np
rand = np.random.RandomState(42)
x = rand.randint(100, size=10)
print(x)
# [51 92 14 71 60 20 82 86 74 74]如果我们想要访问其中三个元素,我们可以这样做:
ind = [3, 7, 4]
x[ind]
# array([71, 86, 60])使用 fancy indexing 的时候,结果的形状与索引数组的形状(而不是原数组的形状)保持一致:
ind = np.array([[3, 7],
[4, 5]])
x[ind]
# array([[71, 86],
# [60, 20]])Fancy indexing 也支持多维数组,看下面这个例子:
X = np.arange(12).reshape((3, 4))
# array([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]])和一般的索引类似,第一个索引对应行,第二个索引对应列:
row = np.array([0, 1, 2])
col = np.array([2, 1, 3])
X[row, col]
# array([ 2, 5, 11])我们可以把普通索引与 fancy indexing 一起使用:
X[2, [2, 0, 1]]
# array([10, 8, 9])
X[1:, [2, 0, 1]]
# array([[ 6, 4, 5],
# [10, 8, 9]])我们还可以把掩码和 fancy indexing 一起使用:
mask = np.array([1, 0, 1, 0], dtype=bool)
X[row[:, np.newaxis], mask]
# array([[ 0, 2],
# [ 4, 6],
# [ 8, 10]])排序
np.sort np.argsort 基本就是数组排序的全部内容了,NumPy 中的 np.sort 比 Python 的 sort sorted 要快的多。如果需要进行局部排序参见 np.partition 的内容,这里不在赘述了。
Python Data Science, NumPy 1
2017 March-18
NumPy(Numerical Python 的简称)提供了 Python 中高效计算的数据结构以及丰富的数据处理方法。Numpy 的 array 和 Python 的 list 接口非常相似,但 Numpy 却要比 list 快的多。NumPy 目前几乎是 Python 整个数据科学工具体系的核心,所以无论数据科学的哪个方面对你感兴趣,花费时间来学习使用 NumPy 的是非常值得的。
我们这里要讲的 NumPy 版本为 1.11.1 可以通过如下的方法在 Python 中查看:
import numpy
numpy.__version__然后使用 NumPy 的时候基本都是用 np 作为引入的缩写:
import numpy as np所以后面如果看到 np.xxx 的地方就知道是在用 numpy 了。
NumPy 这一章节包含两部分内容,一部分讲述其基础数据结构,里面涉及了一些很基础的、大家可能还没有深究的问题,比如为什么它比 Python 的 list 快很多、为什么它用起来和 list 非常相似,这也是这部分重点介绍的部分。另一部分就是介绍 NumPy 中都包含了什么基本的函数,这一部分的很多内容都可以通过文档查询的到,不过这里会讲述一些常用的以及让人迷惑的函数的用法。
虽然我已经尽量略去了那些额外的示例以及大部分人很少涉及到的犄角旮旯,但是这一部分依然会被分割为两个部分进行讲解,这一部分介绍了 NumPy 的基本数据结构以及其快速运算的原理以及基本的数据操作,下一部分介绍 NumPy 的广播运算、高级索引以及排序。
Python 的数据类型
Python Int 不仅仅是 Int
Python 属于动态类型语言,其变量在声明时是不需要定义其类型的,并且一个变量也可以被赋值为任意类型。比如:
x = 4
x = "four"在 Python 中是合法的,而在 C 这样的静态类型语言中这样就会报错:
int x = 4;
x = "four";动态类型增加了 Python 的易用性,但在实际运算的过程中 Python 的解释器总是要知道当前的这个变量到底存储的是什么类型以便进行相应的计算的,因此 Python 的变量不仅仅包含了数值,也包含了其类型的信息。
默认的 Python 语言是由 C 语言编写,并且 Python 的变量就是一个 C 的结构体。例如当我们在 Python 中定义一个整型:x = 100000,x 不是一个纯粹的整数,它是一个指向一个 C 语言结构体的指针。如果我们查看 Python 3.4 的源码就可以看到实现 Python 中的整型(实际上是长整型)的代码如下(其中的一些 C 语言宏已经被展开了):
struct _longobject {
long ob_refcnt;
PyTypeObject *ob_type;
size_t ob_size;
long ob_digit[1];
};可以看到,除了保存了真正的数据的 ob_digit 之外,Python 还保存了引用计数器、类型、数据长度这三个信息。
List 也不仅仅是数组
Python 的 list 中的每一个元素可以是不同的类型,比如:
L3 = [True, "2", 3.0, 4]是合法的。不过在这里灵活性在需要进行大量的数据操作的时候就成为了一种负担:为了允许动态类型,list 中的每一个元素都需要包含它自己的类型信息、引用计数以及其他信息。在这里所有的变量的类型是一样的,每个元素所包含的类型信息是冗余的,如果可以用固定类型数组来保存则会高效的多。
NumPy 数组
与 Python list 不同,NumPy array 的所有元素类型相同。如果类型不同 NumPy 会进行类型转换(这里,整型被转为浮点类型):
np.array([1, 2, 3, 4], dtype='float32')如上,我们可以利用 Python 的 list 来创建 Numpy 的数组,也可以利用 NumPy 提供的函数来创建数组:
np.zeros(10, dtype=int) # 创建一个长度为 10,数据类型为整型,数据全为 0 的数组
np.ones((3, 5), dtype=float) # 创建一个 3x5 的二维数组,数据类型为浮点型,数据全为 1
np.full((3, 5), 3.14) # 创建一个 3x5 的数组,数据全为 3.14
# 创建一个由线性序列填充的数组
# 从 0 到 20,步长为 2
# 与 Python 内建的 range 方法类似
np.arange(0, 20, 2)
# 创建一个从 0 到 1 均匀分割为 5 个元素的数组
np.linspace(0, 1, 5)
# 采用均匀分布创建一个 3x3 的数组
# 默认均匀分布范围从 0 到 1
np.random.random((3, 3))
# 采用高斯分布生成的值填充的 3x3 的数组
# 其中高斯分布的均值为 0 标准差为 1
np.random.normal(0, 1, (3, 3))
# 创建一个采用 [0, 10] 分为的随机数填充的 3x3 的数组
np.random.randint(0, 10, (3, 3))
# 创建一个 3x3 的单位矩阵
np.eye(3)
# 创建一个未初始化的数组,其中的值为所分配的内存的值
np.empty(3)Universal Functions
NumPy 之所以成为了 Python 数据科学的基础在于其提供了一整套高效计算的方案,前面提到了其固定类型数组所带来的好处,这一部分讲述其通过 universal functions 实现的向量化操作。
默认的 Python 循环是非常缓慢的,虽然有一些其他的 Python 编译方案想要让 Python 的执行速度变得快起来,但是其普及程度都远不如默认的 CPython。例如下面的一个求倒数操作,Python 的执行速度慢的令人发指:
import numpy as np
np.random.seed(0)
def compute_reciprocals(values):
output = np.empty(len(values))
for i in range(len(values)):
output[i] = 1.0 / values[i]
return output
values = np.random.randint(1, 10, size=5)
big_array = np.random.randint(1, 100, size=1000000)
%timeit compute_reciprocals(big_array)
# 1 loop, best of 3: 205 ms per loop事实证明,这里的瓶颈不是操作本身,而是 CPython 在循环的每个周期必须进行的类型检查和函数调度。每次计算倒数时,Python 首先检查对象的类型并查找适合该类型的函数来执行计算。如果我们是在编译型的语言中,类型在代码执行之前就已知,那么计算速度就会快得多。
对于许多类型的操作,NumPy 提供了执行这种针对静态类型的编译型的操作,这被称为向量化运算。这可以通过简单地对整个数组执行操作来实现,这相当于对每个元素应用操作。这种向量化方法旨在将循环推入编译层,这是 NumPy 高效运算的基础。看一看对 big_array 的执行速度,与 Python 循环相比,我们看到了数量级的飞跃:
%timeit (1.0 / big_array)
# 100 loops, best of 3: 4.14 ms per loopNumPy中的向量化操作通过 ufuncs 实现,其主要目的是加速 NumPy 数组中的重复操作。与等价的 Python 循环相比使用 ufuncs 的向量化运算基本上都是要快一些,在数组规模比较庞大的时情况下更是如此。当你在 Python 中看到了循环你就应当考虑它是否应当替换为一个向量化的操作。
大多数 Python 的基本运算 NumPy 都对其进行了向量化,即都有对应的 ufuncs:
| Operator | Equivalent ufunc | Description |
|---|---|---|
+ |
np.add |
Addition (e.g., 1 + 1 = 2) |
- |
np.subtract |
Subtraction (e.g., 3 - 2 = 1) |
- |
np.negative |
Unary negation (e.g., -2) |
* |
np.multiply |
Multiplication (e.g., 2 * 3 = 6) |
/ |
np.divide |
Division (e.g., 3 / 2 = 1.5) |
// |
np.floor_divide |
Floor division (e.g., 3 // 2 = 1) |
** |
np.power |
Exponentiation (e.g., 2 ** 3 = 8) |
% |
np.mod |
Modulus/remainder (e.g., 9 % 4 = 1) |
还有一些额外的函数,这里仅仅展示其中的一部分:
# 绝对值
np.abs(x)
# 三角函数
np.sin(x)
# 指数函数
np.exp(x)
np.power(3, x)
# 聚合操作
x = np.arange(1, 6)
np.add.reduce(x)
# 15
np.multiply.reduce(x)
# 120
# 外积操作
x = np.arange(1, 6)
np.multiply.outer(x, x)
# array([[ 1, 2, 3, 4, 5],
# [ 2, 4, 6, 8, 10],
# [ 3, 6, 9, 12, 15],
# [ 4, 8, 12, 16, 20],
# [ 5, 10, 15, 20, 25]])NumPy 数组的基本操作
NumPy 的数组操作和 Python 的 list 非常的类似,这里从以下几个方面进行介绍:
- 数组的属性:长度,维度,内存占用大小,元素的类型
- 数组的索引:获取或修改数组中的单个元素
- 数组的切片:获取或修改数组中的子数组内容
- 数组的重塑(reshape等操作):更改一个数组的形状
- 数组的连接与分割:连接多个数组或者将单个数组分割为多个数组
NumPy 的基本属性
.ndim维度.shape每个维度的长度.size整个数组的长度,等于各个维度长度之积.dtype内部数据的类型.itemsize每个元素的字节长度.nbytes整个数组的字节长度,等于.itemsize * .size
例子:
x = np.random.randint(10, size(3, 4))
print x.ndim
print x.shape
print x.size
print x.dtype
print x.itemsize
print x.nbytes其结果:
2
(3, 4)
12
int64
8
96NumPy 的索引
NumPy 数组的索引和 list 基本一致,也是从零开始计数,也支持负数索引,不过在多元数组时采用逗号分隔的 tuple 类型进行索引(list 采用多个方括号的方式,比如 a[1][2]):
x1 = np.random.randint(10, size(10))
x1[0]
x1[5] = 8
x1[-1]
x2 = np.random.randint(10, size(3, 4))
x2[1, 0]
x2[0, 0] = 12当然,NumPy 数组中的类型是一致的,因此赋值其他类型会被强制转换:
x1[0] = 3.14 # 会被转换为 3NumPy 的数组切片
NumPy 数组也支持用 : 进行切片操作(slicing),切片的参数格式为
[start:stop:step]其中如果 start 没有提供则为 0,如果 stop 没有提供则为当前维度的长度,如果 step 没有提供则为 1:
x = np.arange(10)
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
x[:5]
# [0, 1, 2, 3, 4]
x[4:7]
# [4, 5, 6]
x[::2]
# [0, 2, 4, 6, 8]
x[1::2]
# [1, 3, 5, 7, 9]当 step 为负数时 start 和 stop 的默认值互换。这也是一种将数组倒序的方式:
x[::-1]
# [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
x[5::-2]
# [5, 3, 1]在对多维数组进行切片时不同维度通过逗号分隔:
x2 = np.random.randint(10, size=(3, 4))
# array([[9, 2, 7, 6],
# [2, 6, 1, 1],
# [9, 0, 0, 8]])
x2[:2, :3]
# array([[9, 2, 7],
# [2, 6, 1]])
x2[:3, ::2]
# array([[9, 7],
# [2, 1],
# [9, 0]])
x2[::-1, ::-1]
# array([[8, 0, 0, 9],
# [1, 1, 6, 2],
# [6, 7, 2, 9]])对二维数组获取其某一行或者某一列可以通过全切片与索引配合使用:
print(x2[:, 0]) # 第一列
print(x2[0, :]) # 第一行
print(x2[0]) # 第一行,后面的全切片可以省略注意 NumPy 的切片是一个引用,而不是像 list 里面的是一个拷贝:
x2_sub = x2[:2, :2]
print(x2_sub)
# [[9 2]
# [2 6]]
x2_sub[0, 0] = 99
print(x2)
# [[99 2 7 6]
# [ 2 6 1 1]
# [ 9 0 0 8]]在处理大规模的数组的时候,这种操作不会带来大量额外的内存开销。在需要使用拷贝的时候可以用下面的方式进行:
x2_sub_copy = x2[:2, :2].copy()数组的重塑
重塑,即修改数组的维度信息。比如把一个长度为 9 的一维数组变为一个 3x3 的二维数组:
np.arange(9).reshape((3, 3))要注意,在 reshape 时其创建的新的数组的 size 必须和之前的数组一致。reshape 会尽量采用非拷贝的方式来处理初始数组,但是在初始数据没有提供连续的内存空间的时候就无法实施。类似的方法会在处理图像数据时很常见。
重塑方法另一个常用的情况是将一个一维的数组转换为一个二维的行或者列矩阵。可以通过 reshape 或者 newaxis 方法实现。
x = np.array([1, 2, 3])
# 用 reshape 创建一个 shape 为 (1, 3) 的二维数组
x.reshape((1, 3))
# 用 np.newaxis 创建一个 (1, 3) 的二维数组
x[np.newaxis, :]
# 用 reshape 创建一个 (3, 1) 的二维数组
x.reshape((3, 1))
# 用 newaxis 创建一个 (3, 1) 的二维数组
x[:, np.newaxis]类似的转换比较常见,尤其是在做机器学习算法中需要将数据扩充为多维数组时。
数组的连接与分割
一维数组的连接:
x = np.array([1, 2, 3])
y = np.array([3, 2, 1])
np.concatenate([x, y])
# array([1, 2, 3, 3, 2, 1])
z = [99, 99, 99]
print(np.concatenate([x, y, z]))
# [ 1 2 3 3 2 1 99 99 99]二维数组的连接:
grid = np.array([[1, 2, 3],
[4, 5, 6]])
np.concatenate([grid, grid])
# array([[1, 2, 3],
# [4, 5, 6],
# [1, 2, 3],
# [4, 5, 6]])
# 按照第二维连接
np.concatenate([grid, grid], axis=1)
# array([[1, 2, 3, 1, 2, 3],
# [4, 5, 6, 4, 5, 6]])在数组维度不一致的情况下采用 np.vstack 与 np.hstack 更清晰一些:
x = np.array([1, 2, 3])
grid = np.array([[9, 8, 7],
[6, 5, 4]])
# 按照行连接(垂直连接)
np.vstack([x, grid])
# array([[1, 2, 3],
# [9, 8, 7],
# [6, 5, 4]])
y = np.array([[99],
[99]])
# 按照列连接(水平连接)
np.hstack([grid, y])
# array([[ 9, 8, 7, 99],
# [ 6, 5, 4, 99]])类似地,np.dstack 会按照数组的第三维连接。
与连接相反的操作是分割,通过 np.split,np.hsplit,np.vsplit 实现。通过传递一个索引数组说明分割的位置:
x = [1, 2, 3, 99, 99, 3, 2, 1]
x1, x2, x3 = np.split(x, [3, 5])
print(x1, x2, x3)
# [1 2 3] [99 99] [3 2 1]N 个分割点会生成 N + 1 个子数组。 np.hsplit 与 np.vsplit 类似:
grid = np.arange(16).reshape((4, 4))
upper, lower = np.vsplit(grid, [2])
print(upper)
print(lower)
# [[0 1 2 3]
# [4 5 6 7]]
# [[ 8 9 10 11]
# [12 13 14 15]]
left, right = np.hsplit(grid, [2])
print(left)
print(right)
# [[ 0 1]
# [ 4 5]
# [ 8 9]
# [12 13]]
# [[ 2 3]
# [ 6 7]
# [10 11]
# [14 15]]类似地, np.dsplit 会按照数组的第三维分割。
聚合操作
NumPy 支持各种聚合函数,比如 np.max np.min np.sum np.median 这些方法一看就懂,不再一一列举。不过一个比较让人迷惑的点在于如何按照不同的维度进行聚合。
M = np.random.random((3, 4))
print(M)
# [[ 0.22051857 0.27287109 0.96337129 0.78381157]
# [ 0.24552893 0.39914065 0.70804662 0.80235189]
# [ 0.33662843 0.65632293 0.25875078 0.52569568]]M.sum()默认的 sum 是将所有维度的值加在一起,而聚合函数接受一个额外的参数 axis 用与指定沿着哪一个维度进行计算。例如我们想要按照列去找每一列的最小值就需要指定 axis=0:
M.min(axis=0)
# array([ 0.66859307, 0.03783739, 0.19544769, 0.06682827])结果返回四个值,对应四列的最小值。类似的我们可以找到每一行的最大值:
M.max(axis=1)
# array([ 0.8967576 , 0.99196818, 0.6687194 ])axis 是指那个将要被处理的维度,而不是将要返回的维度。因此指定 axis=0 意味着第一个维度是要被处理的维度:对于二维数组磊说,这意味着每一列的数据将要被聚合。也就是说指定的 axis 最终会被变成 1,例如这里的一个 3x4 的数组,如果指定 axis=0 那么第一维会变成 1 所以会成为一个 1x4 的数组,那么就是每一列做了聚合。类似地,如果 axis=1 那么数组会变成一个 3x1 的数组,那么数组就是按照行做了聚合。
大多数聚合函数都能够处理 NaN 数值的情况:计算过程中会忽略这些 NaN 数据,很多对于 NaN 处理的函数是在 NumPy 1.8 之后添加的,旧版本并不支持。
有关测试的读书笔记
2016 December-06
刚刚培训结束,培训的不少时间是用来看各种乱七八糟的书籍。其中一个重要的领域就是有关测试的部分。这里整理一下前一阵子的笔记。
tdd by example
首先读了一本非常经典的书籍:tdd by example 也是测试驱动开发的由来了。不是第一次读这本书,但是这次读了之后依然有新的体会。读的时候就觉得书中的第一部分的小步都太小了,很多实现都是显而易见的。然而讽刺的是我自己在走这个例子的时候却因为步子太大而忘记在构造函数中设置 MoneyType 反而拖慢了进度。很小的步子隐含了按着步骤走可以大大减少中间出错而打乱节奏甚至是需要 debug 的风险,而debug 所花费的时间与小步走所花费的时间相比绝不是一个数量级的。在练习的过程中细细的去想为什么要这么写以及为什么是这么一个重构的流程引发了我找到了一些其他的书籍逐渐弄明白了书中很多忽略了的细节。比如第一部分中对 expression 钱包的隐喻其实并不是 tdd 所带来的好处,而是因为作者本身有这个设计思维,所以 tdd 不是所带来的益处。
另一个被很多人忽略的点在于每次在写一个测试之前是有一个 task 列表的。tdd 要求你每次写测试之前都知道自己想要实现的功能是什么,而让这个测试的通过就代表某一个小的功能的完成。列出系统想要什么样子并且可以有一个测试对应,这就是在做设计了,这就是 tdd 带来的主要好处吧~可是做不出来设计怎么办?那就是 ooad 的能力问题了。在有了测试之后就用最直接最简单的办法去实现,实现的方式有三种:
- fake 用假实现或者是空实现,等到必须要去实现的时候再实现
- obvious implementation 显而易见的实现,功能是实现了,不过采用的是最简单的办法,在未来可能会有性能问题,对其他的测试可能也不友好
- triangle 三角法,在不好实现的时候才使用的技巧,比如对于一个迭代实现,首先是单个元素的实现,然后逐步改为递归。在之前接触的一些 tdd 培训里面有些教练就认为应当用这种方法实现所有的 tdd 现在觉得有点过了。
实现之后 tdd 讲要做重构。这里的重构和 重构 那本书里面讲的很多是一致的。但是我之前在对重构的粒度和范围的理解确实不到位。通过各种形式的消除重复(代码重复、数据重复)把一个 fake 的实现逐渐转化为一个实际的方案才是重构的核心。
所以 tdd 是对重构的能力有很高的要求的。在之后的读书过程中逐渐的发现,重构是一个非常强大的技术,它不仅仅是在技术层面,在领域层面也是一个很好的工具。仔细想想一个复杂的,需要多年运行和维护的软件如何才能保证代码与架构不腐化堕落呢?唯有坚持重构了吧。
art of unit test
这本书其实主要讲的是单元测试而不是测试驱动开发。开篇它提到了 tdd 所需要的三种核心技能:
- 编写好的单元测试的能力,也就是这本书所讲的内容
- 通过测试驱动开发的能力,也就是 tdd by example 的内容
- 设计的能力,是很多其他设计书籍的内容,这里它推荐了一本书 Growing Object-Oriented Software, Guided by Tests
这本书还明确的定义了什么是单元测试:不是那种一个函数对应一个测试,而是对一个最小工作单元的测试。小巨人的培训里也是强调每个测试是完成了某个功能,这个测试就是这个功能的文档。它定义了一些好的单元测试的特性:
- 自动化
- 容易实现,几分钟
- 在一定时间内有意义,比如第二天,当然它强调的是单元测试而不是函数测试,不应随着重构而随意变化
- 可以一键运行
- 速度很快
- 结果稳定
- 完全隔离,独立于其他测试
它还强调了单元测试与集成测试的区别:集成测试结果不稳定、速度缓慢、多个真实依赖。比如依赖数据库、依赖文件系统。过多的依赖导致的是不能明确的指导什么导致了测试的失败。这也让我开始反思自己以前写的很多与数据库相关测试了。
还有它提出了优秀测试的支柱:
- 只测试一个关注点
- 测试多个方面会导致你的测试命名出现问题
- 一旦第一个测试挂了,后面的断言就不再执行
- 避免在测试中出现逻辑
- 不测试内部方法:一个工作单元都是以一个公共 API 开始,最后达到三种结果中的一个或者多个,返回值、系统状态改变或者第三方调用
- 不滥用 setup 方法,在保证测试的可读性与过度重构测试之间做权衡
Growing Object-Oriented Software, Guided by Test
这本书的思想正如标题所示,通过测试驱动建立面向对象的软件。它认为好的设计是可以通过测试一步步驱动出来的。但是它依然强调事先要知道一些基本的面向对象设计原则,这也是大家的共识吧。
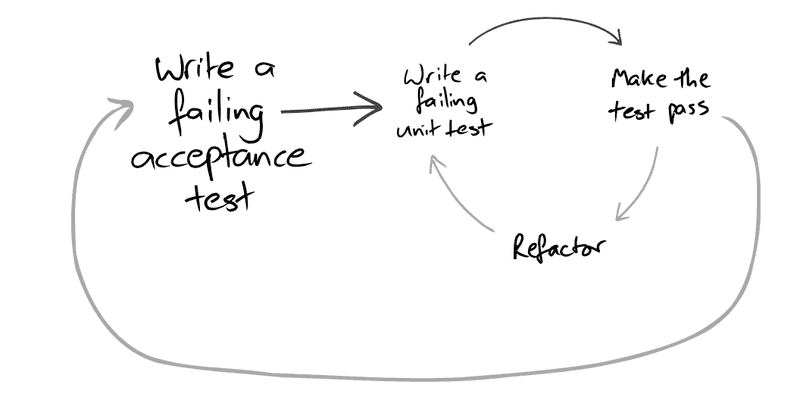
书中提到了要将验收测试和单元测试结合起来,通过大循环套小循环来完成测试。
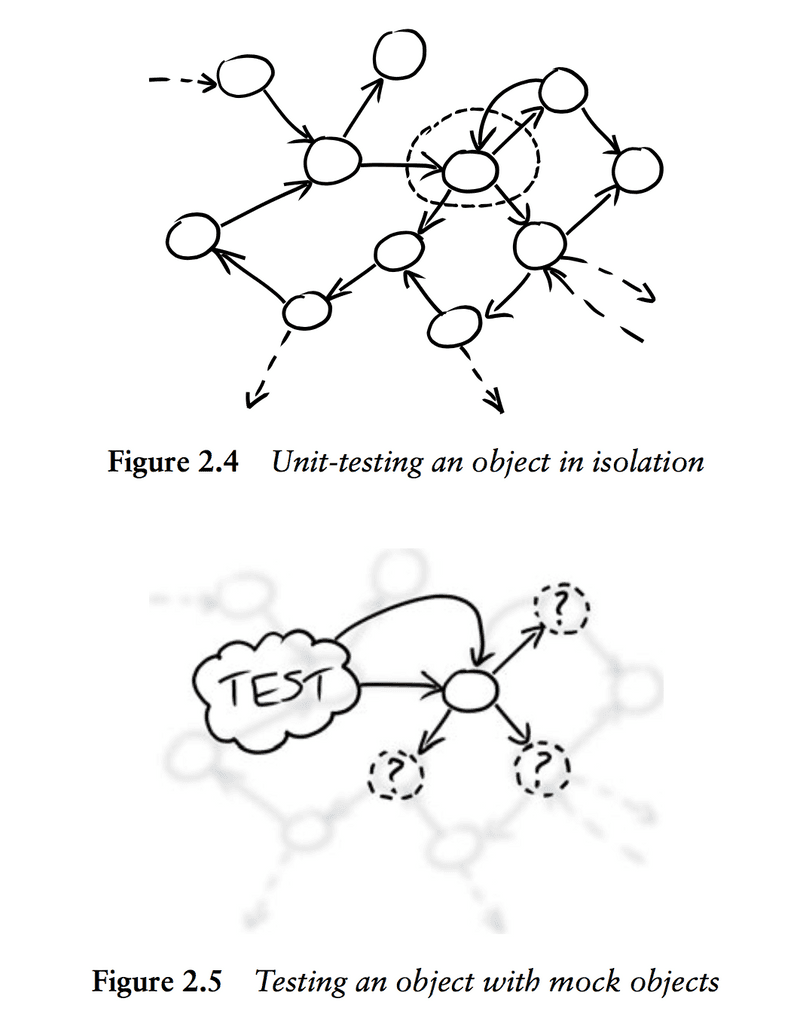
书中提到了通过 mock 和 stub 来隔离各个对象之间的依赖,这个其他几本书中也有所提及。
然后提到了一个对象出现的几个方式:
- breaking out: 将一个大对象拆分成几个相互合作的小对象
- budding off: 提出一个目前的对象所需要的服务,然后用一个对象去负责提供这个服务
- bundling up: 提供一个容器对象去隐藏相关对象的细节
在 TDD 的时候 breaking out 和 budding off 的动作会比较多。
测试驱动开发的艺术
这本书有点像是一个 cookbook。很多思想其他的书中都讲到了,我也没有留下非常深的印象。在有关 web 测试与数据库测试方面有一些值得记录的地方。
tdd for web
对于 mvc 来说 m 是不涉及任何 web 框架的,所以不用提。但是 c v 就是具体问题具体分析了。其中 c 的测试主要是依靠 request 与 response 的 mock。但是结合我目前前后端分离,后端都是 rest api 的情况来说更多的是采用类似于集成测试的方式。那什么叫类似呢?
- 会启动一个临时的 server 从外面去访问这个 api
- 但是所以来的一些东西可能是 fake 的,比如数据库、比如 session、比如外部系统
然后在测试 controller 的时候 view 就随着一起测试了。毕竟都是 json 而已。
tdd for database
首先说明了 db 的 tdd 用 unit test 是没有意义的,因为和数据库如此强依赖,把数据库 mock 掉感觉就没再测什么了。但是,如果每次测试都启动一个 mysql 也是听蛋疼的。所以这里人家采用了类似 fake 的方式:引入一个 memory database。这个是我应该学习的。之前都是直接连接 mysql 这也导致在 docker 里面启动 mysql 的情况。
在 teardown 做清理,采用 tx.rollback()